CAIDA LIBRE

CLASE TEÓRICA Y PRÁCTICA DE CINEMATICA (CAIDA LIBRE)

FÍSICA GRADO 10°

CLASE 1

CLASE 2

CLASE 3

CLASE 4

CLASE 5

CLASE 6

CLASE 7

EJERCICIOS DE CINEMATICA GRADO 10° LAE

1. Una locomotora necesita 10 s. para alcanzar su velocidad normal que es 60 Km/h. Suponiendo que su movimiento es uniformemente acelerado ¿Qué aceleración se le ha comunicado y qué espacio ha recorrido antes de alcanzar la velocidad regular?

2. Un cuerpo posee una velocidad inicial de 12 m/s y una aceleración de 2 m/s2 ¿Cuánto tiempo tardará en adquirir una velocidad de 144 Km/h?

3. Un móvil lleva una velocidad de 8 cm/s y recorre una trayectoria rectilínea con movimiento acelerado cuya aceleración es igual a 2 cm/s2. Calcular el tiempo que ha tardado en recorrer 2,10 m.

4. Un motorista va a 72 Km/h y apretando el acelerador consigue al cabo de 1/3 de minuto, la velocidad de 90 Km/h. Calcular a) su aceleración media. b) Espacio recorrido en ese tiempo.

5. En ocho segundos, un automóvil que marcha con movimiento acelerado ha conseguido una velocidad de 72 m/s. ¿Qué espacio deberá recorrer para alcanzar una velocidad de 90 m/s?

6. Se deja correr un cuerpo por un plano inclinado de 18 m. de longitud. La aceleración del móvil es de 4 m/s2; calcular a) Tiempo que  tarda el móvil en recorrer la rampa. b) velocidad que lleva al finalizar el recorrido inclinado.

7. Dos móviles se dirigen a su encuentro con movimiento uniformemente acelerado desde dos puntos distantes entre sí 180 Km. Si se encuentran a los 9 s de salir y los espacios recorridos por los móviles están en relación de 4 a 5, calcular sus aceleraciones respectivas.

8. Un avión despega de la pista de un aeropuerto, después de recorrer 1000 m de la misma, con una velocidad de 120 Km/h. Calcular a) la aceleración durante ese trayecto. b) El tiempo que ha tardado en despegar si partió del reposo c) La distancia recorrida en tierra en el último segundo.

9. Un móvil se mueve con movimiento acelerado. En los segundos 2 y 3  los espacios recorridos son 90 y 100 m respectivamente. Calcular la velocidad inicial del móvil y su aceleración.

10. Dos cuerpos A y B situados a 2 Km de distancia salen simultáneamente uno en persecución del otro con movimiento acelerado ambos, siendo la aceleración del más lento, el B, de 32 cm/s2. Deben encontrarse a 3,025 Km. de distancia del punto de partida del B. Calcular a) tiempo que tardan en encontrarse, b) aceleración de A. c) Sus velocidades en el momento del encuentro.

CINEMATICA: MOVIMIENTO RECTILÍNEO

LEY DE COULOMB (Electrostática)

Estudiantes Grado 11º:

Leer y analizar la siguiente lectura y realizar los ejercicios de aplicación propuestos al finalizar el texto.

Ley de Coulomb

El físico francés Charles Coulomb investigó en la década de 1780 la relación cuantitativa de las fuerzas eléctricas entre objetos cargados. Su ley la demostró usando una balanza de torsión, que él mismo inventó, identificando cómo varía la fuerza eléctrica en función de la magnitud de las cargas y de la distancia entre ellas.

Esta ley estableció nuevos principios eléctricos hallados por el. Su ley la formulo tras efectuar algunos experimentos que se resumen a continuación.
Para esta ley usó pequeñas esferas con distintas cargas de las que no conocía la carga exactamente, sino la relación de las cargas. Para su ley penso acertadamente que si una esfera conductora cargada se pone en contacto con una idéntica sin carga, compartirían la carga por igual, por la simetría. Para su ley con esto tenía la manera para producir cargas iguales a ½, ¼, etc., respecto a la carga original. Manteniendo constante la separación entre las cargas, observó que si la carga en una esfera se duplicaba, la fuerza se duplicaba; y si la carga en ambas esferas se duplicaba, la fuerza aumentaba a cuatro veces su valor original. Si variaba la distancia entre las cargas, encontró que la fuerza disminuía con el cuadrado referido a la distancia entre ellas, esto es, si se duplicaba la distancia, la fuerza bajaba a la cuarta parte en su valor original.
Esta ley postula que la fuerza eléctrica entre dos partículas cargadas estacionarias es:

• inversamente proporcional al cuadrado aplicado a la separación r entre las partículas y está dirigida a lo largo en la línea que las une.
• proporcional al producto en las cargas q₁ y q₂.
• atractiva si las cargas tienen signo opuesto y repulsiva si las cargas tienen igual signo.

Esta ley también se expresa en forma de ecuación como:

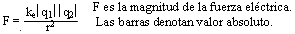
Esta ley ha sido comprobada con avanzados dispositivos, encontrándose que el exponente 2 tiene una exactitud probada en 1 parte en 10¹⁶.
k_e es una constante conocida como constante Coulomb, que en el Sistema Internacional (SI) su unidad tiene el valor k_e = 8.987x10⁹ Nm²/C².
Esta constante también se escribe en la forma 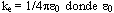 es la constante conocida como permitividad en el espacio libre y su valor es 8.8542x10^-12 C²/Nm².
La unidad por carga eléctrica en el SI es el Coulomb.
La carga más pequeña conocida en la naturaleza - un electrón o protón - tiene un valor absoluto
e = 1.60219x10^-19 C.
Así, una carga con 1 Coulomb es aproximadamente igual a 6.24x10¹⁸ (= 1C/e) electrones o protones.
Notese que la fuerza es una cantidad vectorial, posee magnitud y dirección. Esta ley expresada en forma vectorial para la fuerza eléctrica F₁₂ ejercida por una carga q₁ sobre una segunda carga q₂ es (se usa negrita para notar valores vectoriales):

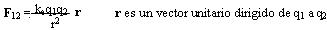
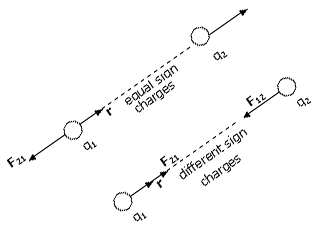
Como toda fuerza sigue la tercera ley Newton, la fuerza eléctrica ejercida por q₂ sobre q₁ es igual en magnitud a la fuerza ejercida por q₁ sobre q₂ y en la dirección opuesta; esto es, F₂₁ = - F₁₂.
Si q₁ y q₂ tienen el mismo signo F₁₂ toma la dirección r. Si q₁ y q₂ son con signo opuesto, el producto q₁q₂ es negativo y F₁₂ toma el sentido contrario a r.
Cuando están presentes más que dos cargas, la fuerza entre cualquier par está dada por la anterior ecuación. Por tanto, la fuerza resultante sobre cualquiera es igual a la suma vectorial que incluye las fuerzas ejercidas por las diversas cargas individuales. Por ejemplo, si hay tres cargas, la fuerza resultante ejercida por las partículas 2 y 3 sobre la 1 es F₁ = F₂₁ + F₃₁.

Ejemplo de su Aplicación

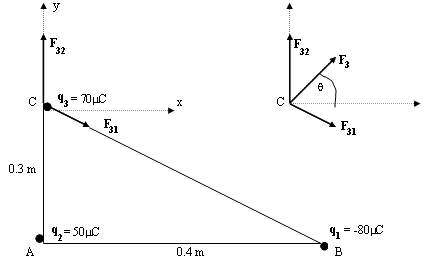
Suponga que se tiene tres cargas puntuales localizadas en los vértices de un triángulo recto, como se muestra en la figura, donde q₁ = -80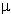 C, q₂ = 50 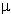C y q₃ = 70 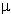C, distancia AC = 30 cm, distancia AB = 40 cm. Calcular la fuerza sobre la carga q₃debida a las cargas q₁ y q₂.

Las direcciones de las fuerzas sabemos coinciden con las líneas que unen a cada par de cargas puntuales. La fuerza que q₁ ejerce sobre q₃, F₃₁, es de atracción. La fuerza que q₂ ejerce sobre q₃, F₃₂, es de repulsión. Así, las fuerzas F₃₁ y F₃₂ tienen las direcciones que se indican. La separación entre q₃ y q₁ se obtiene de (CB)² = (AC)² + (AB)² = (0.3 m)² + (0.4 m)², de donde CB = 0.5 m.

Las magnitudes de tales fuerzas son:

F₃₁ = [(9x109 Nm² /C²)(80x10^-6 C)(70x10^-6 C)]/ (0.5 m)²
= 201.6 N

F₃₂ = [(9x109 Nm² /C²)(5 0x10^-6 C)(70x10^-6 C)]/ (0.3 m)²
= 350 N

Conviene disponer ejes coordenados xy tal como se indica en la figura, con el origen en la carga donde deseamos calcular la fuerza resultante, en este caso en q₃.

Llamando F₃ a la fuerza resultante sobre q₃, entonces F₃
= F₃₁ + F₃₂ . Luego, en términos de componentes x e y :

F_3x = F_31x + F_32x
F_3y = F_31y + F_32y
F_31x = F₃₁cos = (201.6 N)x(40/50) = 161.3 N ; F_31y
= - F₃₁sen = -201.6x30/50 = -121 N
F_32x = 0 ; F_32y = F₃₂ = 350 N
F_3x = 161.3 N + 0 = 161.3 N ; F_3y = -121 N + 350 N = 229 N

La magnitud de la fuerza neta F₃ se obtiene de (F₃)²
= (F_3x)² + (F_3y>)², resultando F₃ = 280 N. El ángulo de esta fuerza se obtiene de tg = F_3y/ F_3x= 229/161.3
= 1.42 ==> = 54.8º.

Ejercicio de su Aplicación

Ocho (8) cargas puntuales cuyos valores q1= 3C, q2= 7C, q3= 2C, q4= 9C, q5= 4C, q6= 1C, q7= 4C y q8= 3C, forman un cubo de arista 17 cm, tal y como se muestra en la figura.  

Determine todas las posibles fuerzas eléctricas (28 en total) de atracción o repulsión según sea el caso, que se puedan presentar en el sistema. Suponga que dichas cargas se encuentran sumergidas en aceite.

Indique la dirección de las fuerzas.

NIVELACION FÍSICA GRADO 10° PRIMER Y SEGUNDO PERIODO

Solucionar los siguientes ejercicios y presentarlos en hoja examen con fecha de entrega opcional de acuerdo a sus  capacidades, intereses y responsabilidades.

1. Un vehículo circula a 100 km/h cuando choca contra un muro de hormigón que no sufre aceleración o deformación alguna. Si la deformación que experimenta el vehículo es de 0,6 m, determina el tiempo que tarda el vehículo en detenerse y qué aceleración sufrirán los ocupantes del vehículo.
2. La aceleración de frenado de un coche es de unos 6 . Calcula la distancia de frenado cuando la velocidad del vehículo es de 90 km/h. ¿Cuál es esa distancia si la velocidad es de 120 km/h?
3. Un automóvil circula a 54 km/h y frena hasta detenerse con una aceleración de . ¿Qué distancia recorrerá antes de pararse?
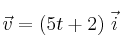4. Sabiendo que la velocidad de un cuerpo es en unidades SI. ¿Cuál será su posición para el instante t = 3 s.
5.  
   Desde un acantilado de 45 m de altura se lanza hacia abajo una piedra con velocidad inicial de 2 m/s. ¿Qué tiempo tardará la piedra en llegar al suelo? ¿Con qué velocidad impactará?
   Dato:
   
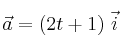6. Sabiendo que la aceleración de una partícula es en unidades SI. Calcula cuál es su desplazamiento en un intervalo de 4 s.
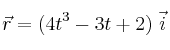7. El vector de posición de una partícula es expresado en unidades SI: a) ¿Cuál es su vector velocidad? b) ¿Y su vector aceleración? ¿Es constante la aceleración? c) Calcula la velocidad de la partícula para el instante t = 5 s. d) ¿Cuál es su aceleración en ese mismo instante?
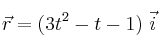8. El vector de posición de una partícula que se mueve según el eje X es . Determina los vectores velocidad y aceleración.
9. Se lanza una pelota verticalmente hacia arriba con una velocidad inicial de 30 m/s. Si su aceleración es de hacia abajo, ¿cuánto tardará la pelota en alcanzar la máxima altura y cuál será su valor?
10. Un pasajero viaja entre Alicante y Edimburgo pero haciendo escala en Bruselas. Si la distancia entre Alicante y Edimburgo es de 1969 km y la escala supone 330 km más de recorrido y ha tardado 4 horas en completar el viaje: a) ¿Cuál es el recorrido que ha realizado el pasajero? ¿Cuál es el desplazamiento? b) ¿Cuál es su celeridad media? ¿Y su velocidad media? 
11.  Un avión realiza un vuelo transatlántico a una velocidad de crucero de 900 km/h. Si la distancia a recorrer son 5 500 kilómetros. a) ¿Qué tiempo tardará en llegar a su destino? b) Si la maniobra de despegue y aterrizaje suponen un total de una hora sobre el tiempo total del viaje, ¿cuál es su celeridad media?
12. Una partícula está en x = 5 m para t = 0 s, en x = -7 m para t = 6 s y en x = 2 m para t = 10 s. Calcula la velocidad media de la partícula durante los intervalos de tiempo: a) De 0 a 6 s; b) de 6 a 10 s y c) de 0 a 10 s. 
13. Un coche se mueve en línea recta con una velocidad media de 95 km/h durante 2 horas y 40 minutos y luego con una velocidad media de 50 km/h durante 1,2 h.a) ¿Cuál es el desplazamiento total?b) ¿Cuál es la velocidad media?
14. En un viaje en coche hemos recorrido 450 km en 6 horas pero decidimos cambiar de sentido y recorremos 20 km en 30 minutos para visitar un monumento. a) ¿Cuál fue la celeridad media del viaje, expresada en km/h? b) ¿Cuál ha sido la velocidad media del viaje en m/s? c) ¿Y la velocidad media de los últimos 20 kilómetros en km/h y m/s?
15. Un corredor hace 100 m en 10 s y luego vuelve andando recorriendo 50 m en 30 s. Calcula la celeridad media y la velocidad media del recorrido total.
16. Un conductor se mueve con velocidad constante entre los puntos A y B, luego su velocidad se hace 16 m/s entre los puntos B y C. Sabiendo que la distancia entre A y B es la misma que entre B y C e igual a 10 000 m, ¿cuál era la velocidad entre los puntos A y B? (El tiempo total del trayecto ha sido de 0,45 horas).
17. Un hombre conduce desde su trabajo a su casa a una velocidad constante de 70 km/h. Cuando han pasado 30 minutos se da cuenta de que se le han olvidado unos documentos en la oficina. ¿A qué velocidad constante tendría que conducir para volver a la oficina en 12 minutos?
18. ¿Qué distancia recorrería un coche que se mueve con una velocidad constante de 80 km/h en 7 min?
19. Un caracol está en la posición 15 mm para el instante 2 s. En el instante 7 s su posición es 9 mm. Determina el desplazamiento y la velocidad media del caracol en el intervalo de tiempo.
20. Desde una ventana a 25 m de altura se lanza una piedra verticalmente hacia arriba con una velocidad de 20 m/s. Determinar: a) La altura máxima que alcanza. b) La velocidad con la que la piedra llega al suelo y el tiempo transcurrido desde que se lanzó. Dato: g = 9,8  
21. Un niño lanza unos caramelos de una altura de 1,75 m con una velocidad inicial de 1 m/s. ¿Cuánto tiempo tardarán los caramelos en llegar al suelo?
22. Una cápsula de aterrizaje puede decelerar con un valor de la aceleración igual a «g». Si la cápsula empieza su maniobra de aterrizaje a una velocidad de 900 km/h, ¿cuánto tiempo tarda en detenerse?
23. Una cápsula de aterrizaje puede decelerar con un valor de la aceleración igual a g. Si la cápsula empieza su maniobra de aterrizaje a una velocidad de 900 km/h, ¿cuánto tiempo tardará en detenerse?
24. Se sostiene un libro de 2 kg de masa desde un balcón situado a 20 m del suelo y, de repente, se suelta. Calcule la distancia recorrida y la velocidad que lleva cuando ha transcurrido 1 s
25. Un conejo corre hacia su madriguera a 72 km/h. Cuando está a 200 m de ella un perro, situado 40 m detrás del conejo, sale en su persecución recorriendo 90 m con una aceleración de 5 y continuando después a velocidad constante. a) ¿Alcanzará el perro al conejo? b) ¿Qué ocurriría si la madriguera estuviera 100 m más lejos? Razone ambas respuestas con ecuaciones.
26. Un saltador de longitud bate con un ángulo de 45º, 10 cm antes de la línea de marca. Si la marca realizada es de 8,90 m. ¿Cuál era su velocidad al iniciar el salto? (Tenga en cuenta que se mide a partir de la línea de marca).
27. Se lanza una pelota al aire con una velocidad inicial de 50 m/s en una dirección que forma 37º con la horizontal. Hallar el tiempo total que permanece en el aire la pelota y la distancia horizontal total que recorre utilizando la aproximación g = 10  
28. El quarterback de un equipo es capaz de lanzar el balón con una velocidad de 30 m/s. Si uno de sus compañeros está a 42 m de él, ¿con qué ángulo debe lanzar la pelota para que éste pueda recibirla?
29. Un tirador dispara su arma contra una diana de 20 cm de diámetro que está situada a 45 m en la misma horizontal. Si la velocidad de salida del proyectil es de 400 m/s, ¿impactará el proyectil sobre la diana si apunta al centro de ésta?
30. Un río fluye de oeste a este con una corriente de 3 m/s. Un nadador nada en dirección norte a 2 m/s. ¿Cuál será la velocidad del nadador con respecto a la orilla?
31. Un avión supersónico vuela horizontalmente a una altura de 20 km y a una velocidad de 2500 km/h. Se le desprende un motor, ¿a qué distancia horizontal del lugar del desprendimiento impactará el motor contra el suelo?
32.  Un barco navega por un río que tiene dirección norte-sur a 60 km/h con respecto a la orilla. Una corriente de 15 km/h le empuja desde el nordeste. ¿En qué dirección tiene que apuntar el barco para viajar en dirección norte?

DÍA DE LA CIENCIA Y LA TECNOLOGÍA PROYECTO CIENTIFICO 2012 - GRADOS 10° Y 11°

Estudiantes grados 10° y 11°:

Los términos de referencia para la elaboración del informe final del proyecto científico para presentar en el año 2012, son:

1. Título
2. Presentación o Introducción
3. Justificación
4. Objetivos (general y específicos)
5. Materiales y/o reactivos
6. Diseño y Metodología
7. Gráficas, esquemas y/o figuras
8. Conclusiones
9. Bibliografía
10. Anexos (si los hay)

Nota: Proyecto a desarrollar en forma individual o máximo en grupos de dos (2) estudiantes. Elaborado a computador, siguiendos normas ICONTEC, fuente Arial 12, espacio 1, las gráficas, esquemas o figuras pueden ir a mano. Fecha de entrega del informe 27 de Septiembre de 2012. Fecha de presentación del proyecto 25 de Octubre de 2012.

Temas opcionales:

• Movimiento rectilíneo
• Movimiento parabólico
• Movimiento circular
• Dinámica
• Estática
• Hidrodinámica
• Movimiento armónico (péndulos y resortes)
• Acústica
• Óptica
• Electrostática
• Eletrodinámica
• Proyectos aplicables a ingeniería o industria.

Estudiantes grado 10º:

Ingresar al siguiente enlace, leerlo con atención y realizar exposición sobre "Movimiento Circular Uniforme y Dinámica del Movimiento Circular", con fecha de presentación  25 de Julio de 2011.  Grupos de 4 estudiantes (ni más ni menos).

http://www.sc.ehu.es/sbweb/fisica/dinamica/circular1/circular1.htm